Training Diverse High-Dimensional Controllers by Scaling Covariance Matrix Adaptation MAP-Annealing

IEEE Xplore arXiv Code (GitHub) Supplemental Video TL;DR (Twitter)

Bryon Tjanaka
University of Southern California
tjanaka@usc.edu

Matthew C. Fontaine
University of Southern California
mfontain@usc.edu

David H. Lee
University of Southern California
dhlee@usc.edu

Aniruddha Kalkar
University of Southern California
kalkar@usc.edu

Stefanos Nikolaidis
University of Southern California
nikolaid@usc.edu

Abstract

Pre-training a diverse set of neural network controllers in simulation has enabled robots to adapt online to damage in robot locomotion tasks. However, finding diverse, high-performing controllers requires expensive network training and extensive tuning of a large number of hyperparameters. On the other hand, Covariance Matrix Adaptation MAP-Annealing (CMA-MAE), an evolution strategies (ES)-based quality diversity algorithm, does not have these limitations and has achieved state-of-the-art performance on standard QD benchmarks. However, CMA-MAE cannot scale to modern neural network controllers due to its quadratic complexity. We leverage efficient approximation methods in ES to propose three new CMA-MAE variants that scale to high dimensions. Our experiments show that the variants outperform ES-based baselines in benchmark robotic locomotion tasks, while being comparable with or exceeding state-of-the-art deep reinforcement learning-based quality diversity algorithms.

Supplemental Video

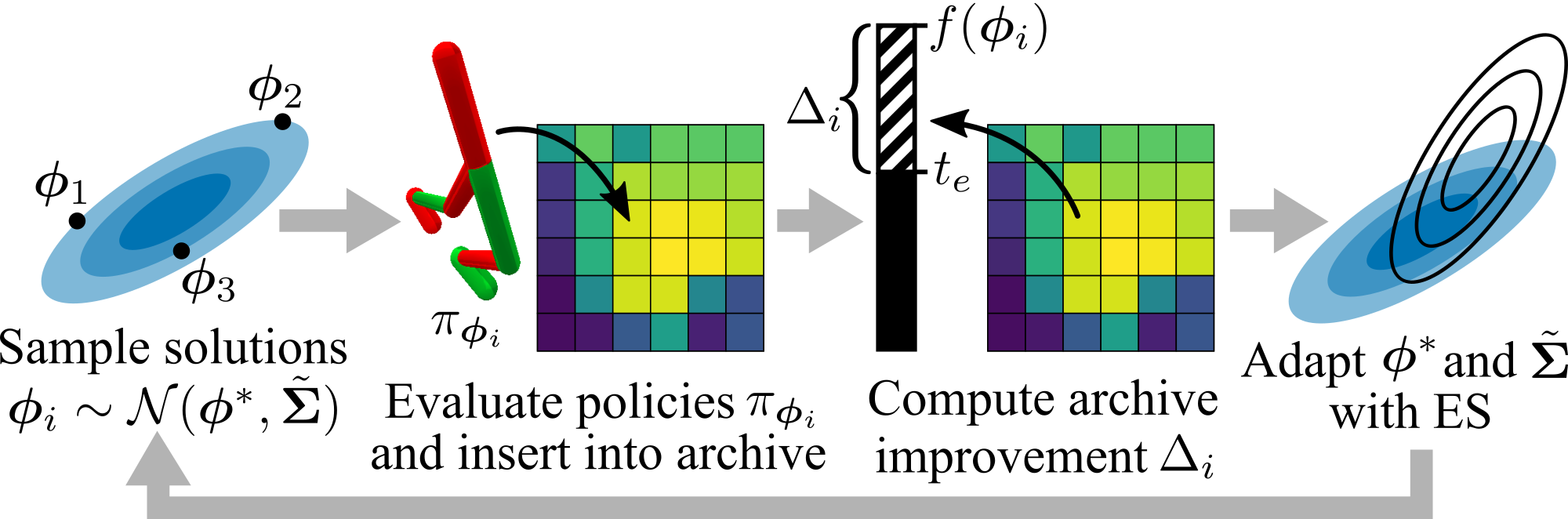
Algorithm Overview

We propose variants of the CMA-MAE algorithm that scale to high-dimensional controllers. The variants maintain a Gaussian search distribution with mean $\bm{\phi}^*$ and approximate covariance matrix $\tilde{\bm{\Sigma}}$. Solutions $\bm{\phi}_i$ sampled from the Gaussian are evaluated and inserted into an archive, where they generate improvement feedback $\Delta_i$ based on their objective value $f(\bm{\phi}_i)$ and a threshold $t_e$ that each archive cell maintains. Finally, the Gaussian is updated with an evolution strategy (ES). Our variants differ from CMA-MAE by incorporating scalable ESs, as the CMA-ES used in CMA-MAE has $\Theta(n^2)$ time complexity per sampled solution.